Valor de verdad
Las tablas de verdad son un elemento de la lógica proposicional para determinar el valor de verdad (es decir, si es “verdadero” o “falso”) de una proposición. Los valores de verdad posibles son dos: verdadero y falso, que también pueden expresarse como 1 y 0. Una proposición sólo puede ostentar uno de ellos (ni los dos a la vez, ni ninguno de ellos). Estos valores se llaman “booleanos” por el álgebra de Boole, que tiene la particularidad de operar con datos binarios (que sólo tienen dos valores posibles).
Normalmente se representa al valor Verdadero con la letra V y al valor Falso con la F. También se usan las letras T (por “true”, “verdadero” en inglés) y F (por “false”, “falso” en inglés).
Proposición
Una proposición es una afirmación capaz de tener un valor de verdad. Es decir, una oración de la cual se puede decir que es verdadera o que es falsa.
Ejemplo 1:
"El día está soleado" (será verdadero o será falso, según si el día está o no está soleado).
Una proposición puede ser: atómica si no puede subdividirse, o molecular si está compuesta por dos o más proposiciones, unidas por un operador lógico.
Ejemplo 2:
Proposición atómica: "El día está soleado".
Proposición molecular: "El día está soleado y caluroso". Es molecular porque puede sudividirse en dos proposiciones: “el día está soleado” y “el día está caluroso”.
Cuando se realizan operaciones con proposiciones, uniéndolas mediante operadores lógicos, se suele dar nombres (usualmente compuestos de una sola letra) a las proposiciones. Esto es para ayudar a la legibilidad. Entonces podríamos decir que la proposición “el día está soleado” se va a llamar “p” y que la proposición “el día está caluroso” se va a llamar “q”. Como tenemos también una proposición molecular que se forma al unir estas dos, podemos darle el nombre “r” a la proposición “el día está soleado y caluroso”.
Operaciones lógicas
Una operación lógica se compone de operandos (proposiciones) y operadores. Mediante una operación lógica se unen proposiciones para obtener una nueva proposición compuesta.
Los operadores lógicos (también llamados “conectores lógicos”) usados para unir proposiciones son: AND (“y”), OR (“o”), NOT (“no”), IMPLICA, BICONDICIONAL (“si y sólo si”). Mediante ellos se forman proposiciones moleculares.
El operador AND se utiliza para la operación conjunción yse representa mediante el símbolo 
El operador OR se utiliza para la operación disyunción y se representa mediante el símbolo 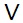
El operador NOT se utiliza para la operación negación y se representa mediante el símbolo 
El operador IMPLICA se usa para la operación implicación (también llamada “condicional”). A la proposición que se coloca a la izquierda del operador se la llama “antecedente” y a la que se coloca a la derecha de la llama “consecuente”. Esta operación no es conmutativa. Se representa mediante el símbolo 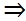
El operador BICONDICIONAL se usa para la operación doble implicación (también llamada “equivalencia”) y se representa mediante el símbolo 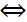
La negación es una operación unaria, porque involucra un único operando (proposición). El resto son binarias, porque involucran dos operandos. Además, pueden unirse más de dos proposiciones, usando más de un operador lógico.
Tabla de verdad de cada operador lógico
Como dijimos, los operadores lógicos unen proposiciones. Entonces, al unir dos proposiciones, se obtiene una nueva proposición, cuyo valor de verdad dependerá de cuáles son concretamente los valores de verdad de las proposiciones unidas. Si, por ejemplo, hoy el día está soleado y además caluroso, podemos decir que la proposición “p” es verdadera y que la proposición “q” también es verdadera. Pero tenemos que ver qué pasa con la proposición “r”, que está compuesta por “p AND q” (es decir, es una conjunción). Para averiguar cuál es ese resultado, se debe conocer el valor de verdad de p (que ya acordamos que, en este ejemplo es Verdadero), el valor de verdad de q (que, en este ejemplo es Falso) y la tabla de verdad de la conjunción. Si el operador lógico fuera OR usaríamos la tabla de verdad de la disyunción, y así siempre usando la tabla de la operación correspondiente.
Las tablas de las operaciones, de acuerdo a las distintas posibles combinaciones de los valores de verdad de los operandos, son las siguientes:
CONJUNCIÓN

Esto se lee:
Cuando p es Verdadero y q es Verdadero, p Y q es Verdadero
Cuando p es Verdadero y q es Falso, p Y q es Falso
Cuando p es Falso y q es Verdadero, p Y q es Falso
Cuando p es Falso y q es Falso, p Y q es Falso
La característica de la conjunción es que sólo es V cuando ambos operandos son V.
DISYUNCIÓN

Esto se lee:
Cuando p es Verdadero y q es Verdadero, p Ó q es Verdadero
Cuando p es Verdadero y q es Falso, p Ó q es Verdadero
Cuando p es Falso y q es Verdadero, p Ó q es Verdadero
Cuando p es Falso y q es Falso, p Ó q es Falso
La característica de la disyunción es que sólo es F cuando ambos operandos son F.
NEGACIÓN
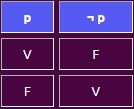
La característica de la negación es que invierte el valor de verdad de la proposición.
IMPLICACIÓN

Esto se lee:
Cuando p es Verdadero y q es Verdadero, p IMPLICA q es Verdadero
Cuando p es Verdadero y q es Falso, p IMPLICA q es Verdadero
Cuando p es Falso y q es Verdadero, p IMPLICA q es Verdadero
Cuando p es Falso y q es Falso, p IMPLICA q es Falso
La característica de la implicación es que sólo es F cuando el antecedente es V y el consecuente es F.
DOBLE IMPLICACIÓN

Esto se lee:
Cuando p es Verdadero y q es Verdadero, p SI Y SOLO SI q es Verdadero
Cuando p es Verdadero y q es Falso, p SI Y SOLO SI q es Falso
Cuando p es Falso y q es Verdadero, p SI Y SOLO SI q es Falso
Cuando p es Falso y q es Falso, p SI Y SOLO SI q es Verdadero
La característica de la doble implicación es que sólo es V cuando ambos operadores tienen el mismo valor de verdad.