Abstraerse es “separar las cualidades de un objeto para considerarlas aisladamente”, ver algo desde otro punto de vista sin prestar atención a sus detalles. Sería como tener una imagen que tiene aplicado mucho zoom, donde vemos concretamente cada pixel bien definido, y luego alejamos ese zoom (nos abstraemos) para poder ver la imagen completa.
Los problemas que se resuelven mediante la programación suelen estar expresados en forma abstracta, pero hay que traducirlos a operaciones concretas que la computadora pueda entender.
Si recordamos que la computadora sólo comprende números y operaciones matemáticas y lógicas, entonces sabremos que hay que construir todo lo demás en base a eso. Por suerte, hay muchísimo ya construido: por ejemplo, en Python no necesitamos construir una instrucción que le permita a la computadora escribir algo en la pantalla porque eso ya fue solucionado cuando alguien “inventó” el print(); nosotros sólo lo usamos. Esta es la diferencia entre el bajo nivel (que es más cercano al lenguaje de máquina) y el alto nivel (que es más cercano al lenguaje humano y suele resumir muchas instrucciones de máquina en una única instrucción de alto nivel).
Usando esas estructuras, instrucciones y tipos de datos que ya alguien construyó previamente, podemos crear nuestros propios algoritmos en base a eso.
La computadora siempre intentará traducir lo que lee a algo que pueda entender. Si lee 8 sabrá que se trata del número 8 (porque ella entiende números). Si lee “hola” sabrá que es una cadena de caracteres (porque cada carácter tiene un código numérico asociado mediante la tabla ascii, entonces internamente la computadora hace la conversión y para ella esa cadena no es más que una sucesión de números). Si lee 9+40, a primera vista no sabe qué resultado da, pero conoce los números por un lado y las operaciones matemáticas por otro, entonces los usa para hacer esa cuenta y obtener el resultado, que es un nuevo número (algo que, como ya dijimos, la computadora entiende). Así que, para la computadora, 9+40 es el número 49. Si luego lee *(20+5)3** empieza nuevamente a ver cómo puede convertir todo eso a un dato concreto: empieza por lo que necesita resolver primero, 20+5, y para ella ahí hay un 25; luego hace 25*3 y así llega a la conclusión de que (20+5)*3 es el número 75. Esto significa que, a eso que nosotros vemos en forma abstracta como una operación matemática, la máquina lo ve concretamente como el número que es su resultado. Es decir, el número 75 podría expresarse de varias formas distintas: el 75 concreto (lo que la computadora necesita para operar) y la operación (20+5)*3 que, al resolverla, resulta en el número 75.
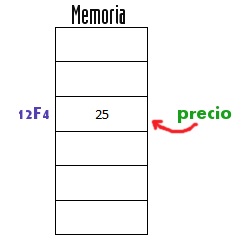
Por otra parte, la computadora “sabe” que tiene una memoria con celdas numeradas (a estos números se les llama “direcciones de memoria”) y cómo acceder lo que hay dentro de esas celdas. Pero nosotros no podemos acordarnos del número de cada celda ni podemos saber en qué celda la computadora guardará cada dato, así que les damos “sobrenombres” a las celdas: estas son las variables. Así, en vez de decirle a la máquina “guardar el número 25 en la celda 12F4” (el número de celda lo representamos en hexadecimal), le decimos “guardar el número 25 en la variable precio”. De esta forma tenemos una abstracción en dos sentidos: la primera es por el nombre, ya que no necesitaremos acordarnos de 12F4 sino de precio; la segunda por la ubicación, ya que el sistema operativo puede ubicar la variable precio donde más le convenga (en la celda 12F4 o en cualquier otra) cada vez que el programa se ejecuta.
Una característica de las variables es que el contenido de una celda puede ir cambiando (varía). Entonces podríamos guardar un dato dentro de una de esas celdas y, en vez de usar el dato concreto, usamos el nombre de la celda. Cuando usemos ese nombre de celda, la computadora nuevamente va a tener que ver qué significa, porque lo que estamos usando es una abstracción: nosotros lo vemos desde un punto de vista más amplio, pero la computadora necesita ir metiéndose dentro de esa abstracción (“haciéndole zoom a la imagen”, siguiendo el ejemplo del principio) hasta llegar a algo que ella comprenda. Y ella sólo entiende de números, entonces “mira” a qué número de celda corresponde el nombre de variable, toma el dato que está en esa celda y lo usa como le indiquemos. ¿Por qué esto es útil? Porque el dato puede variar y yo obtengo siempre el dato actualizado. Por ejemplo, si a la máquina le pido que imprima tengo 21 años, siempre dirá lo mismo. ¡Pero yo todos los años cumplo un año más! Entonces podría guardar en una variable el número 21 (y cada año le cambio ese valor), llamar a esa variable “miEdad” y luego decirle a la computadora que imprima tengo miEdad años, indicándole de alguna manera cuál es el texto que tiene que interpretar literalmente y cuál es la variable. Entonces, para indicarle qué parte del texto es literal, en la mayoría de los lenguajes se lo coloca entre comillas (y la variable se pone sin comillas). Así, las partes que son literales son: “tengo” y “años”. De la misma forma, el número 21 en la oración inicial era un literal, pero como está compuesto sólo por números, no se confunde con el nombre de una variable, entonces no necesita comillas. Por esto es que, en la mayor parte de los lenguajes, los nombres de variables no pueden ser numéricos (no podemos tener una variable que se llame 123 porque la computadora lo interpretaría literalmente como el número ciento veintitrés).
De esta forma, si en una variable llamada primerNúmero (no puede haber espacios en los nombres de variables) se guarda el número 130 y en otra llamada segundoNúmero se guarda el 20, puedo decirle a la computadora que calcule primerNúmero+segundoNúmero y obtener el resultado 150. Así, nosotros vemos una abstracción, porque vemos nombres de variables en vez de los datos concretos, pero la computadora necesita averiguar qué es concretamente esa instrucción, entonces se dedica a buscar en la memoria qué tiene guardado cada una de esas variables para luego poder operar.
Pero la abstracción no funciona solamente convirtiendo nombres de variables en los valores que contienen, o convirtiendo operaciones matemáticas en sus resultados, sino que se aplica también a cualquier otra cosa, reduciendo todo a algo que la computadora entienda. Y así es como la abstracción puede extenderse por muchos niveles. Por ejemplo, en Python hay listas heterogéneas (pueden contener elementos de cualquier tipo de dato), que tienen índices numerados para ubicar sus elementos, comenzando por el orden 0. Entonces, si tuviéramos una lista de tres elementos como esta: [ 7-2+1, “hola”, [unaVariable,otraVariable] ] guardada en una variable llamada lista, podemos usar una abstracción para referenciar al primer elemento: lista[0] pero la computadora, que sólo entiende de posiciones de memoria y números, tiene que resolver esa abstracción hasta obtener algo concreto: va a tener que acceder a la celda de memoria que corresponde a la variable lista en su primera posición (la 0) para poder ver qué representa lista[0] y luego deberá seguir resolviendo la operación matemática 7-2+1 para quedarse, por último, con el número 6. Entonces, donde nosotros vemos lista[0] la computadora ve 6. Para seguir ejemplificando, si en unaVariable tengo guardado el número 4 y en otraVariable tengo guardado el string “buen día”, cuando yo escriba lista[2] la computadora entenderá [4, “buen día”] (que es el elemento [unaVariable,otraVariable] ubicado en el índice 2 de la variable lista).
Para decirlo de forma sencilla: cada expresión que la computadora pueda resolver, se reemplaza por el resultado concreto que la computadora obtiene.
Abstracción y uso de variables
Por todo esto que venimos viendo, podemos deducir que la computadora no podrá entender ningún nombre de variable que no esté en la memoria. ¿Por qué? Simplemente porque, cuando intenta buscar ese nombre de variable en su memoria para averiguar qué valor guarda, no lo encuentra.
Entonces, cada vez que usemos un nombre de variable, tendremos que cuidar que esa variable tenga algún dato guardado. Por ejemplo, si intento mostrar en pantalla el resultado de una suma mediante la instrucción print(4+N) pero la variable N no aparece en el código antes de esta instrucción print, la computadora irá a buscar una variable N en la memoria y no encontrará nada. En cambio, sí va a encontrar algo si me aseguro de que previamente se guarde algún valor en la variable N:
N=leer_numero()
print(4+N)